- Divide: membagi masalah menjadi beberapa upa-masalah yang memiliki kemiripan dengan masalah semula namun berukuran lebih kecil (idealnya berukuran hampir sama),
- Conquer: memecahkan (menyelesaikan) masing-masing upa-masalah (secara rekursif), dan
- Combine: mengabungkan solusi masing-masing upa-masalah sehingga membentuk solusi masalah semula.

Divide and conquer adalah varian dari beberapa strategi pemrograman topdown, tetapi keistimewaannya adalah membuat sub-sub problem dari problem yang besar, oleh karena itu strategi ini ditunjukkan secara berulang-ulang (recursively), didalam menerapkan algoritma yang sama dalam sub-sub problem seperti yangditerapkan pada masalah aslinya (original problem). Sebagaimana prinsip dasar algoritma perulangan dibutuhkan sebuah kondisi untuk mengakhiri perulangan tersebut. Biasanya untuk mengecek apakah problem sudah cukup kecil untuk diselesaikan dengan metode secara langsung. Mungkin dari segi ilustrasi kita, bahwa proses-proses pada komputer paralel tentunya memiliki proses/problem/job yang cukup kompleks sehingga harus dipecah-pecah menjadi sub-sub problem. Selain dibutuhkan sebuah “kondisi”, juga diperlukan “fase divide” untuk membagi/memecah problem menjadi sub-sub problem yang lebih kecil, dan “fase combine“ untuk menggabungkan kembali solusi dari sub-sub problem kedalam solusi dari problem awalnya.
Berikut pseudocode dari strategi divide and conquer

Pseudocode diatas adalah sebagai acuan dari strategi divide and conquer, tetapi dalam implementasinya ada beberapa diferensiasi dari bentuk diatas yang akan digunakan. Sebelum masuk ke pokok pemrograman dengan “Divide and Conquer strategy/algorithm”, ada 4 hal penting yang harus dipahami dalam strategi ini yaitu branching factor, balance, data dependence of divide function dan sequentiality.
Branching Factor
Branching factor dalam algoritma divide and conquer adalah jumlah dari subproblem yang akan dibagi dari sebuah problem awal. Ini adalah langkah nyata dari algoritma divide and conquer, didalam proses pembagian yang sebenarnya, jumlah dari branching factor harus 2 atau lebih, karena jika tidak problem tidak bisa dibagi. Banyak jenis algoritma ini termasuk pula algoritma komputasi geometric yang memiliki branching factor berjumlah 2.
Balance
Sebuah algoritma divide and conquer dikatakan balance jika problem awal dibagi menjadi sub-sub problem dengan ukuran yang sama. Yang artinya jumlah dari keseluruhan ukuran subproblem sama dengan ukuran problem awal (initial problem). Algoritma Mergesort dan binary tree, dan sama halnya dengan algoritma reduksi & prefix sum adalah beberapa contoh algoritma divide and conquer yang seimbang (balance).
Data Dependence of Divide Function
Algoritma divide and conquer memiliki sebuah fungsi pembagian terhadap data yang memiliki ketergantungan, artinya jika ukuran relatif dari sebuahsubproblem tergantung pada proses input datanya. Ini adalah salah satu ciri dari algoritma yang tidak seimbang, salah satu contohnya adalah algoritma quicksort yang akan membagi subproblem dengan fungsi data-dependent divide.
Control Parallelism or Sequentiality
Algoritma divide and conquer dikatakan berurutan (sequential) jika subproblem dieksekusi sesuai dengan perintah program. Paralelisasi dari algoritma divide and conquer yang terurut pertama kali didefinisikan oleh Mou’s Divacon[Mou90], yang terjadi ketika hasil dari salah satu sub-eksekusi diperlukan oleh subeksekusi yang lain. Dalam kasus ini hasil dari subtree pertama diberikan (passing) kepada proses komputasi subtree kedua, supaya hasil akhir tersebut bisa digunakan sebagai nilai awalnya, tetapi sekarang ini contoh diatas tidak dapat dijadikan ilustrasi lagi karena teknologi komputer paralel yang semakin canggih dan kompleks.
Klasifikasi dari Algoritma/Strategi Divide and Conquer
Berikut klasifikasi algoritma divide and conquer, kita bisa melihat daftar dan karakteristik dari beberapa algoritma yang ditunjukkan dalam tabel :

Tabel karakteristik dari Algoritma divide and conquer. Catatan bahwa quicksort
dan quickhull bisa dikonversi kedalam algoritma yang balance dengan cara
menemukan median (titik tengah) yang tepat.
Penerapan Data-Parallel Divide and Conquer Algorithms
Sorting
Quick Sort, Binary Sort
Computational Geometry
Closest Pairs, Convex Hull, Delaunay Triangulation
Graph Theory
Travelling Salesman Problem (TSP), Graph Separators
Numerical
Matrix Multiplication, FFT
Not Data Parallel
Naïve Merge Sort
Rekursi Divide and Conquer
Machiavelli menggunakan sintaks : Split (result1 = func (arg1), result2 = func (arg2) [, resultn = func (argn)]) Untuk membentuk fungsi call dalam algoritma divide and conquer. varn adalah hasil akhir yang kembali ke fungsi func dalam argument argn. Machiavelli membuat versi fungsi yang salah satunya mengaplikasikan reduksi menjadi sebuah “pengulangan sederhana” . Script berikut adalah contoh pemakaian fungsi fetch :

Penerapan fetch untuk integer
Script diatas dapat digunakan untuk meng-compile algoritma parallel dari versi serial. Script berikut menunjukkan contoh lain dimana lebih efisien dalam penerapannya yaitu Quicksort :

Contoh Penerapan Pada Binary Search
Temukan sebuah elemen atau bilangan pada array yang telah tersortir :
1. Divide : cek elemen tengah
2. Conquer : secara rekursif, cari disebuah subarray
3. Combine : trivial
Kasus :
Temukan bilangan 9 pada deret 3, 5, 7, 8, 9, 12, 15

Contoh Penerapan Bucket Sort Secara Paralel
Asumsikan sebuah p processor menangani setiap bucket (p bucket)
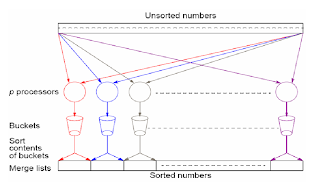
Penjelasan
Bagilah secara sekuen kedalam m bagian, bagian-bagian yang terbentuk akan ditangani oleh p processor, Masing-masing processor akan menangani p bucket dan memisahkan bilangan bilangan pada array ke dalam masing-masing bucket. Bucket-bucket akan dikosongkan kedalam p bucket akhir dari pengurutan yang membutuhkan masing-masing processor untuk mengirim sebuah bucket untuk setiap processor lainnya (bucket i to processor i )
Contoh Lain Penerapan Bucket Sort Secara Paralel
Pada contoh ini dikenalkan sebuah operasi message-passing yang baru all-to-all broadcast.

Penjelasan
Bagilah secara sekuen kedalam m bagian, bagian-bagian yang terbentuk akan ditangani oleh p processor, Masing-masing processor akan menangani p small bucket dan memisahkan bilangan-bilangan pada array ke dalam masing-masing small bucket. Masing-masing small bucket dari masing-masing processor akan dikosongkan, kemudian hasil perhitungan di small bucket akan ditampung ke masing-masing large buket. Di large bucket data diolah kembali untuk kemudian dihasilkan array yang telah tersortir dari masing-masing large bucket.
“all-to-all” broadcast routine
Mengkomunikasikan data dari masing-masing proses ke proses lainnya

all-to-all” routine pada dasarnya mentransfer baris-baris dari sebuah array ke kolomkolom yang dinamakan Transpose Matrix.
Kesimpulan :
Algoritma divide and conquer sudah lama diperkenalkan sebagai sumber dari pengendalian proses parallel, karena masalah-masalah yang terjadi dapat diatasi secara independent. Banyak arsitektur dan bahasa pemrograman parallel mendesain implementasinya (aplikasi) dengan struktur dasar dari algoritma divide and conquer.
Divide and Conquer secara umum terbagi dalam tiga fase, divide yakni membagi masalah kedalam sub-sub masalah yang lebih kecil, conquer yakni menyelesaikan sub-sub masalah secara rekursif, dan combine menggabungkan hasil dari penyelesian sub-sub masalah menjadi penyelesaian yang dikehendaki Terdapat empat hal pada strategi “divide and conquer” : branching factor, balance, data dependence of divide function dan sequentiality.


Tidak ada komentar:
Posting Komentar